Dal punto di vista della simmetria, quando guardiamo un disegno piano, oppure qualcosa di tridimensionale, l’oggetto algebrico che lo caratterizza è il suo gruppo di simmetria, ovvero l’insieme di tutte le isometrie del piano (o dello spazio) che mandano il disegno (rispettivamente, l’oggetto 3d) in se stesso.

Partiamo per esempio da un disegno che si ripeta nel piano con una traslazione (come questo, che dobbiamo immaginare prolungato all’infinito sia a destra che a sinistra); il suo gruppo di simmetria contiene solo traslazioni: di 1 passo, di 2 passi, …, di n passi,… , ma anche di 0 passi (che corrisponde a star fermi), e di 1 passo all’indietro, o di un arbitrario numero di passi all’indietro, … Immaginiamo ora di identificare, come fossero un sol punto, tutti i punti che differiscono per un elemento del gruppo (in matematica questo insieme di punti si chiama orbita e da questa parola proviene il nome orbifold, che sta per orbit manifold, ovvero varietà delle orbite).
Se fissiamo (per esempio) il punto corrispondente all’estremo dell’alluce di un dato piede, la traslazione di un passo porta questo punto nell’estremo dell’alluce del piede successivo, … la traslazione di sette passi lo porta nel punto corrispondente del piede che è ubicato sette passi più in là, e così via.
Quindi identificare a un sol punto tutti i punti dell’orbita significa avere un solo punto estremo di alluce a rappresentare tutti i punti che sono l’estremo dell’alluce in tutti i piedi.

Naturalmente dobbiamo fare questa operazione non solo per l’estremo dell’alluce, ma anche per le altre dita, o per un particolare punto del tallone, ecc.; per capire cosa si ottiene alla fine di questo processo, possiamo individuare una zona di piano che contiene un solo piede, che potrebbe essere una striscia verticale della larghezza di un passo, e osservare che in questa striscia tutti i punti all’interno (della striscia) producono punti diversi nel quoziente (non si trova una traslazione che mandi l’uno nell’altro due punti all’interno della striscia), ma dobbiamo ancora identificare fra loro le due rette che la delimitano (e che si ottengono l’una dall’altra proprio con una traslazione di un passo).
In conclusione otteniamo un cilindro; e questo cilindro rappresenta il quoziente del piano rispetto al gruppo di simmetria del disegno (lo chiameremo anche quoziente del disegno, riferendoci così anche al motivo – qui un solo piede – che troveremo disegnato sul cilindro). Anche in disegni di questo tipo il quoziente è un cilindro. La cosa bella è che possiamo immaginare questo cilindro come un “timbro” (come il rullo del pittore) che, opportunamente decorato con un certo motivo, riproduce sul piano il disegno da cui siamo partiti.

È proprio questo che ci dice che il quoziente è un punto di vista “importante”: è quello che contiene, condensate, tutte le informazioni necessarie per ricostruire il disegno da cui si è partiti.
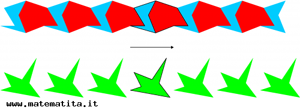
Anche partendo dal disegno delle orme lasciate da una camminata normale, e volendo individuarne il quoziente, arriveremmo a isolare una striscia di piano limitata da due rette parallele: questa volta, però, per mandare una striscia (che contiene p.es. l’orma di un solo piede destro) nella successiva (che contiene l’orma di un piede sinistro) non ci vuole una traslazione, ma piuttosto una glissoriflessione. Quindi ancora le due rette parallele che delimitano la striscia vanno identificate, ma questa volta si identificano “alla viceversa”: il risultato non è più un cilindro, ma un nastro di Moebius.

Vediamo un altro esempio. Inserendo alcune mattonelle in una camera di specchi si vede un disegno che ha un certo gruppo di simmetria; per scoprire come è fatto il quoziente del piano rispetto a questo gruppo, fissiamoci su un dato punto, per esempio il centro di uno dei quadrati piccoli (verde): esso andrà identificato a tutti i centri di tutti i quadrati piccoli verdi (perché comunque si fissino due quadrati verdi, si trova sempre un’isometria che non muta il disegno – quindi sta nel suo gruppo di simmetria – e manda i due quadrati verdi, e quindi anche i loro due centri, l’uno nell’altro); ma il centro di un quadrato verde non andrà identificato, per esempio, al centro di uno dei quadrati arancione grossi (perché NON c’è una simmetria del gruppo che fissi il disegno e che mandi questi due punti l’uno nell’altro); se poi spostiamo la nostra attenzione su un vertice del quadratino verde, scopriamo che con una rotazione di 90° intorno al centro del quadratino (e si tratta di una rotazione che fissa il disegno globale!) possiamo mandare questo punto, volta a volta, negli altri vertici dello stesso quadrato; sicché nel quoziente avremo un solo punto a rappresentare tutti i 4 vertici del quadrato.

In conclusione, il quoziente è proprio il triangolo individuato dalla camera di specchi e anche questa, come il rullo del pittore, funziona da “timbro” che ha la possibilità di riprodurre sul piano un disegno con questo tipo di simmetria: il “motivo”, che corrisponde al disegno con cui inchiostrare il rullo, è costituito in questo caso dalle mattonelle che si inseriscono nella camera di specchi.

Un ultimo esempio: un’immagine di questo tipo ha un gruppo di simmetria assai più semplice: le trasformazioni che fissano la figura sono solo 4 e sono le 4 rotazioni che hanno tutte centro nello stesso punto, al centro della figura, e angoli rispettivamente 90°, 180°, 270° e 360° (quest’ultima è la rotazione di 0°, cioè l’identità che lascia tutto fermo). Come è fatto il quoziente? Basta prendere un settore di 90°, centrato nel centro della figura, e identificare le due semirette che costituiscono il bordo di questo settore, ottenendo così un cono.

È facile anche immaginare altri esempi analoghi a questo: per il gruppo di simmetria di questa figura, la situazione è quasi uguale, salvo il fatto che l’apertura del cono corrisponde questa volta a un angolo di 120° anziché di 90°, mentre in quest’altro caso avremo un cono più “stretto”, corrispondente a un angolo di 45°. Anche questi coni si possono immaginare come dei timbri; se li decoriamo con un certo motivo e li inchiostriamo, allora potremo utilizzarli in modo da riprodurre sul piano un disegno che ripete il motivo inchiostrato sul cono un certo numero di volte, a seconda dell’apertura del cono: usando lo stesso cono e cambiando il motivo usato per inchiostrarlo, otteniamo disegni diversi, ma con lo stesso tipo di simmetria.