non solo ipercubi
Perché solo 6?

Se vogliamo costruire un poliedro regolare, partiamo con l’utilizzare come facce dei poligoni regolari, tutti uguali fra loro, e li assembliamo intorno a un vertice in modo che (nel piano) resti una fessura, ovvero in modo che la somma degli angoli che arrivano in quel vertice sia strettamente minore di 360°.
È proprio questa fessura che permette di richiuderli poi nello spazio tridimensionale e di ottenere un poliedro convesso (se la somma degli angoli fosse uguale a 360° si otterrebbe una tassellazione piana).
È così che possiamo convincerci che i poliedri regolari non sono più di 5, perché le combinazioni possibili sono solo 5: pentagoni a 3 a 3, quadrati a 3 a 3, triangoli a 3 a 3, oppure a 4 a 4, oppure a 5 a 5.
Naturalmente per essere sicuri che i poliedri regolari sono esattamente 5 dovremmo poi far vedere che ognuna di queste combinazioni intorno a un vertice si può portare avanti, sempre nella stessa maniera, fino a ottenere un poliedro.
Proviamo a mimare per analogia questo ragionamento in dimensione superiore, ovvero cerchiamo di costruire un politopo regolare nello spazio a 4 dimensioni; possiamo cominciare a scegliere un poliedro regolare e poi provare ad assemblare varie copie di questo poliedro regolare, tutte uguali fra loro, intorno a uno spigolo. Abbiamo bisogno però che resti una fessura (nello spazio 3d), ovvero che la somma degli angoli diedri che arrivano in quello spigolo sia minore di 360°; come per i poligoni che si assemblano in poliedri, sarà proprio questa fessura che garantisce che si possa poi richiuderli nello spazio 4d e ottenere un politopo convesso (se la somma degli angoli diedri fosse uguale a 360° si otterrebbe una tassellazione dello spazio: si pensi ad esempio a 4 cubi intorno a uno spigolo).
Anche in questo caso le possibilità non sono molte.
Se partiamo da tetraedri regolari, possiamo metterli insieme a 3 a 3 oppure a 4 a 4, oppure a 5 a 5, non di più perché l’angolo diedro di un tetraedro regolare è maggiore di 60°.
|
Se partiamo da cubi, possiamo metterli insieme a 3 a 3 e non di più perché l’angolo diedro di un cubo è 90°, sicché mettendoli insieme a 4 a 4 otterremmo una tassellazione dello spazio.
|
|
|
Se partiamo da ottaedri regolari, possiamo metterli insieme a 3 a 3 e non di più perché l’angolo diedro di un ottaedro regolare è maggiore di 90°.
|
|
|
Se partiamo da dodecaedri regolari, possiamo metterli insieme a 3 a 3 e non di più perché l’angolo diedro di un dodecaedro regolare è maggiore di 90°.
|
Se partiamo da icosaedri regolari, non possiamo metterli insieme nemmeno a 3 a 3 perché l’angolo diedro di un icosaedro regolare è maggiore di 120°.
Ci sono quindi al massimo sei possibilità, e si può in effetti dimostrare che in ciascuno di questi sei casi si può continuare questo assemblaggio finché si richiude (nello spazio quadridimensionale) in un politopo convesso:
- l’ipertetraedro, composto da 5 tetraedri (3 intorno a ogni spigolo);
- l’iperottaedro, composto da 16 tetraedri (4 intorno a ogni spigolo);
- il 600-celle, composto da 600 tetraedri (5 intorno a ogni spigolo);
- l’ipercubo, composto da 8 cubi (3 intorno a ogni spigolo);
- il 24-celle, composto da 24 ottaedri (3 intorno a ogni spigolo);
- il 120-celle, composto da 120 dodecaedri (3 intorno a ogni spigolo).
non solo ipercubi
Non solo ipercubi
Ci sono in queste pagine molte figure, animazioni, approfondimenti relativi all’ipercubo e si potrebbe essere spinti a pensare che l’ipercubo sia il solo possibile oggetto in dimensione 4...: non è così! Si tratta solo dell’oggetto più semplice e quindi di più facile descrizione, ma nello spazio a 4 dimensioni esiste uno “zoo” di figure altrettanto e più vario dell’analogo “zoo” in dimensione 3.
In primo luogo ci sono i 6 politopi regolari, ovvero gli analoghi dei 5 poliedri platonici in dimensione 3, uno dei quali è l’ipercubo.
Ma ci sono anche altre possibilità, così come nel mondo tridimensionale dei poliedri esistono i prismi e le piramidi, esistono i poliedri uniformi, esistono i poliedri stellati, così tutte queste famiglie di oggetti - e molte altre ancora - si possono anche definire e studiare nel mondo 4D.
Una delle animazioni qui presentate si riferisce proprio a un politopo regolare stellato, e precisamente all’analogo quadridimensionale del grande icosaedro ; nell’animazione questo politopo attraversa un mondo 3d e quello che noi vediamo è la sezione: come se un abitante di flatlandia vedesse i diversi poligoni che si formano nel suo mondo piatto quando un icosaedro stellato lo attraversa.
Non c’è da stupirsi che all’inizio si vedano diversi poliedri“staccati” e che sembrano un po’ assomigliare al grande icosaedro stellato: se immaginiamo di sezionare il grande icosaedro stellato con un piano ortogonale alla direzione vertice-vertice si formerebbe come sezione una stella regolare a 5 punte, mentre se lo tagliassimo
con un piano ortogonale alla direzione faccia-faccia apparirebbero all’inizio tre stelle, staccate, che non sarebbero proprio delle regolari stelle a 5 punte, ma apparirebbero un po’ distorte.
Che altro c’è nel mondo 4d? Non ci saranno solo gli analoghi dei poliedri, ma anche gli analoghi delle superfici? Le sfere ad esempio? Certamente ci sono, e anzi gli analoghi delle superfici presentano una ricchezza di forme molto più varia rispetto alla relativa monotonia delle superfici.
Limitiamoci qui alla sfera: l’ipersfera nello spazio 4d si può definire come la sfera nello spazio 3d (e come la circonferenza nel piano) ovvero come il luogo dei punti equidistanti da un punto fissato, che sarà il centro dell’ipersfera. Ma come ce la possiamo immaginare? In un certo senso il nostro mondo 3d è una ipersfera a patto che si immagini di “chiuderlo” con un punto all’infinito.
Per dar senso a questa affermazione si pensi di appoggiare una sfera a un piano e di proiettare poi la sfera sul piano dal polo Nord (ovvero dal punto antipodale rispetto al punto di tangenza fra sfera e piano): otteniamo una corrispondenza biunivoca - che si dice proiezione stereografica - fra tutto il piano e “quasi” tutta la sfera, ovvero tutta meno il polo Nord. In modo del tutto analogo possiamo ottenere una corrispondenza biunivoca - che si chiama ancora proiezione stereografica - fra il nostro spazio 3d e l’ipersfera meno un punto.
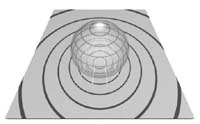
Possiamo allora proiettare nello spazio 3d (e quindi “vedere”) degli oggetti contenuti nell’ipersfera. È proprio così che sono state realizzate alcune delle animazioni qui proposte: in questa ad esempio si immagina di proiettare un 120-celle sulla ipersfera circoscritta (come si può immaginare di “gonfiare” un dodecaedro sulla sfera circoscritta ) e poi, usando la proiezione stereografica, si può passare dalla ipersfera allo spazio 3d e immaginare quindi di “entrare” letteralmente in un 120-celle.
Naturalmente le facce non sono più proprio dodecaedri regolari, esattamente come qui le facce del dodecaedro disegnato sul piano non sono proprio dei pentagoni; ma questi sono gli inconvenienti delle proiezioni...!