Quanti sono i poliedri uniformi, e come sono fatti?

Intanto ci sono i cinque poliedri regolari.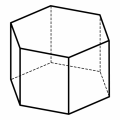

Un altro esempio molto comune (anzi una famiglia di infiniti esempi) si trova fra i prismi: un prisma retto che abbia per base un poligono regolare è un poliedro uniforme di tipo (4,4,…) non appena l’altezza del prisma è tale che le facce laterali risultino dei quadrati

Ci sono quindi infiniti poliedri uniformi tra i prismi, uno per ogni poligono regolare che si fissi come base (in particolare, se la base è un quadrato, si ritrova il cubo): in figura è rappresentato un (4,4,6).

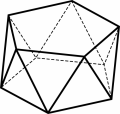C’è un’altra famiglia di poliedri - forse meno conosciuti - che contiene al suo interno infiniti poliedri uniformi, ed è la famiglia degli antiprismi: in figura è rappresentato un antiprisma uniforme di tipo (3,3,3,5), in cui in ogni vertice arrivano un pentagono regolare e tre triangoli equilateri.
È facile immaginare come, anche partendo da un poligono regolare con un numero arbitrario di lati anziché dal pentagono regolare, si possa trovare un poliedro uniforme (in particolare, se la base è un triangolo equilatero, si ritrova l’ottaedro).

Ci sono altri poliedri uniformi oltre ai prismi, agli antiprismi, e ai poliedri regolari? Quanti e quali? Ce ne sono, ma non sono molti: tredici in tutto, che a volte vengono chiamati “poliedri archimedei”. Se vogliamo descriverli tutti usando - come già abbiamo fatto - il simbolo numerico, l’elenco completo può essere organizzato nella seguente tabella:

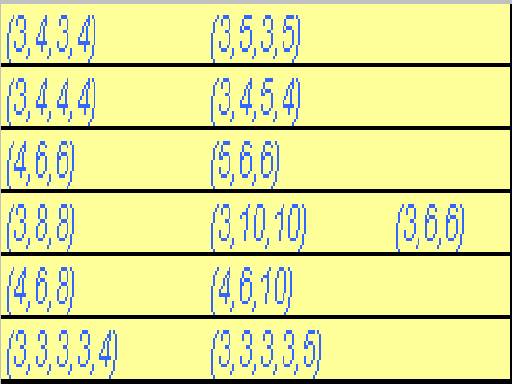
Il modo con cui la tabella è costruita può aiutare a capire la genesi di questi numeri, e di questi poliedri. I poliedri della prima colonna hanno a che fare con il cubo, quelli della seconda hanno a che fare con il dodecaedro, l’unico poliedro nella terza colonna ha a che fare con il tetraedro.
Quasi tutti i poliedri della prima colonna hanno in effetti lo stesso tipo di simmetria del cubo (e quindi, in particolare, si possono vedere in un caleidoscopio, usando il caleidoscopio associato al cubo); solo il poliedro dell'ultima riga ha un tipo di simmetria che è (parente di quello del cubo, ma è) diverso perché contiene solo rotazioni (e, quindi, non si riesce a vedere in un caleidoscopio).
Allo stesso modo, tutti i poliedri della seconda colonna, eccetto l’ultimo, si vedono nel caleidoscopio del dodecaedro, e quello nell’ultima colonna si vede nel caleidoscopio del tetraedro.
Non è neanche casuale nella tabella la sistemazione per righe. Ad esempio, il poliedro (3,8,8) rappresentato qui sotto in figura si ottiene da un cubo “smussandone” i vertici, e curando di farlo in modo tale da ottenere triangoli equilateri e ottagoni regolari. I due poliedri nella stessa riga di (3,8,8) si ottengono con l’identica costruzione, variando però il poliedro di partenza: per ottenere un (3,10,10) si parte dal dodecaedro e per ottenere un (3,6,6) si parte dal tetraedro. Qualcosa di analogo succede anche per le altre righe.

Gli osservatori delle regolarità numeriche possono anche aver notato che i simboli della seconda colonna si ottengono dai corrispondenti nella prima colonna cambiando alcuni “4” in “5” e gli “8” in “10”. Come si spiega? E perché nel (3,4,4,4) si cambia in un “5” solo il “4” centrale e non gli altri due? L’osservazione delle figure qui sotto può suggerire una risposta….