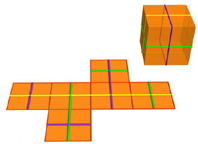
When we point to a picture like this and say that it is a hypercube, we are leaving out something important. To discover the properties of a hypercube, we must clarify what it is that we have left out. In fact, the picture is not that of a hypercube, which is a four-dimensional object, but that of a net of a hypercube, which is a three-dimensional object (and the picture, of course, is only a two-dimensional representation of that three-dimensional object). This three-dimensional net is related to the real four-dimensional object in the same way that this plane surface consisting of six squares is related to a cube.
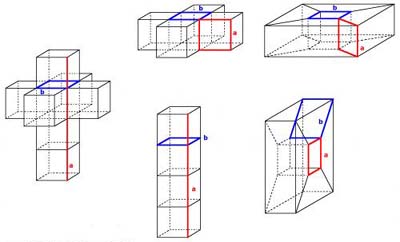
The plane surface becomes a cube when the faces are folded out of the plane and the boundary edges are identified two by two. In a similar way, we can decide which edges of the net are to be identified.

The eight cubes of the net fold into a hypercube when certain boundary faces are identified and glued together two by two. This time too, we can decide which squares in the net may be identified.
Of course, not all arrangements of eight cubes (octacubes) are nets of a hypercube (just as not all figures composed of six squares form the net of a cube). For instance, this is not a net of a hypercube. The problem is that there are there four cubes adjacent to the same edge. It is similar to the analogous situation of placing four squares adjacent to a vertex in the plane in trying to form the net of a cube. Even if we could leave the plane and move into three-dimensional space, we could not fold the figure into a cube because we would be prevented from doing so by that vertex.

There are 11 nets of a cube altogether and there are 261 nets of a hypercube. This video shows some of these 261 nets. They are obtained from one another by allowing the cubes to roll along the octacube in analogy to how we could obtain the 11 nets of a cube by removing one square and gluing it somewhere else (at a valid place, of course). An interactive animation shows all the nets. If you click on a face of a net, the octacube changes; a part comes off and is glued back along the square that has been clicked. Note that you should not click on just any face, but only on a square that is adjacent to an edge where three cubes come together. You can detect the clickable squares by the fact that they light up when they are selected. Another animation proposes to compare a fixed net and other five ones: you must recognize the fixed one among the others. It is not at all a trivial task!

How do we know that there are 11 nets of a cube and 261 nets of a hypercube? And in general, how can we discover all the nets of a given polyhedron or polytope (a polytope is the generalization of a three-dimensional polyhedron to other dimensions)? The answer to the first question is easy. You can obtain them “by hand” by examining all possible figures made up of six squares. The answer to the second question is more complicated, but in principle can be worked out in the same way as the first question. The answer to the third question is more surprising even in three-dimensional space, never mind bothering about four dimensions. If you enjoyed finding out that there are 11 nets of a cube, you can easily discover the two nets of a regular tetrahedron, and with a little effort, the eleven nets of a regular octahedron . On the other hand, you will be in for a lot of work if you try to count all possible nets of a dodecahedron or a icosahedron by hand. In both cases, there are 43380 of them.

Let us take a string with free ends and try to knot it as we wish. We can make a simple knot, or a knot like those depicted in Milan in the central mosaic of the Galleria, or a running knot, or any other knot suggested by our imagination or our expertise of sailors, taylors, etc.
If we do not join the free ends of the string, it is always possible to unknot it with a little bit of patience - even if we tied it very tightly, which is not very convenient in this case! We just need to let one of the loose ends go back following the knot.
After making any knot (or even after making nothing), let us try to join in some way the ends of the string by glueing them or by attaching a magnet to each of them and, after that, letting the two ends come together - it would be desirable not to make a new knot for this operation so that the original knot and the new "technical" knot will not be confused. In this way, we fix the knot "once and for all": for example, if you tie the string of a simple knot, by joining the ends , you will find the trefoil knot. We can lay it on a table in various ways which are different from that in the picture, but it will always be the trefoil if you do not cut the string.
If, on the contrary, we knot a string and get one of the knots like those in the central octagon in the Galleria, in Milan, we find a knot which is called the “figure eight Knot” after tying the two ends of the string.
If, finally, we don’t knot a string at all, we will get a more or less circular knot after tying the two ends of the string: it is the unknot.

Now, let us try to manipulate these knots without pulling away the two joined ends. If we move them, "knotting" them more and more, we will realize the following:

• it is not possible to obtain the trefoil from the unknot and the unknot from the trefoil;
• it is not possible to obtain the trefoil from the figure eight knot and vice versa;
• it is possible to make any "groove" to the unknot and deform it back to the circle without cutting the string, which is not possible for the "real" knots;
• it is possible to obtain the unknot from the running knot and viceversa, in fact the running knot is the unknot!

The list might go on ......

If we tie a string and join the two ends of it, we "catch" in some way the real essence of a knot. Once we join the two ends, it does not matter what kind of manipulations we make provided we do not cut the string: the knot will always be the initial one.

Now, you may try to reproduce the various knots on the poster A knotty issue from the exhibition matemilano. For this purpose, it is useful not to get confused by the under/over specifications at the various crossings on the two branches of the string. If you exchange one of them, the knot you will obtain may be completely different! Some diagrams may seem to be different at first sight; however they represent the same knot. For instance, among the diagrams on the poster there are three of them which represent the trefoil (this is the first, this is the second and this is the third). Three other knots represent the figure eight knot (this is first, this is the second and this is the third), e and finaly other three, besides the circle, which represent the unknot (this is the first, this is the second one and this is the third one).
On the contrary, some diagrams, which may look different at first sight, represent different knots. For instance, three among these pictures have the same "shadow", but they represent the figure eight knot, the trefoil and the unknot respectively.

As soon as the knot becomes more complicated, it is not easy at all to understand "before one's very eyes" if two knots are the same or not, and if a knot is the unknot or a real knot. You might have tried to disentangle a ball of wool fallen on the floor. If you imagine to join the ends of the ball, you may have an idea of how difficult it is to decide whether the knot is real or not.
Actually, it is even more complicated than what you might think. Not only is it difficult to realize "before one's very eyes" whether two knots are the same or not, but nobody has hitherto found an algorithm that can solve this problem in general!. In other words, the classification of knots is still an open problem in Mathematics.

Let us imagine to be an ant on a cube. The ant is in the middle of one of the six square faces. It moves toward the center of one of the four adjacent faces and, after that, it goes “straight ahead”. “Straight ahead” is in inverted commas because the ant does not move on a straight line. It must move on the surface of the cube, so sometimes there are right angles on its path.
It is easy to realize that the ant goes back to the starting point after moving on four squares which form a sort of a “ring”. The four squares are all the faces of the cube except two, which are opposite one to the other.
On a cube there are three different rings like the one mentioned before.
What happens on a hypercube? What kind of path will a hyper-ant describe if it starts from the center of one of the eight cubic faces and goes “straight ahead” aiming at the center of one of the six adjacent cubes?

The path described by the hyper-ant closes up this time as well. The hyper-ant goes back to the starting point after passing on four cubes. The chain of four cubes can be visualized quite well on a net of the hypercube. In particular, it is clearer on a net where there are four cubes one over the other. When we make all the identifications and pass to the four-dimensional world, we must recall that, on the column of four cubes, the bottom face of the bottom cube is glued to the upper face of the upper cube. In this way, the four cubes form a doughnut. Surprisingly, the cubes “avoided” by the ant form a doughnut too, which is linked to the previous one. This can be well visualized in some nets of the hypercube. This means that the hypercube splits in two linked doughnuts, each of four cubes.

How many doughnuts of this kind are there in a hypercube? We can start from a cube and point out that there is a doughnut - which contains the cube - for each of the three directions orthogonal to two opposite faces in the cube. Since there are 8 cubes, we obtain 24= 8 × 3 doughnuts. Each of these doughnuts is counted 4 times, one for each of the cubes in it. In other words, there are six different doughnuts in a hypercube.

In the animation about the hyper-ant you can see the six different possible paths, that is to say, the six possible doughnuts of four cubes in a hypercube (and the three possible decomposition of a hypercube in two pairs of doughnuts). On the left of the screen, the “environment” of the hypercube is described under stereographic projection.The hypercube is enflated on a hypersphere which is next projected on three-dimensional space. On the right of the screen, you can follow the same paths on a net of the hypercube. The colours are not randomly chosen. They highlight the directions of the two-faces. The 24 squares in the hypercube are coloured with six different colours; for each colour there are 4 (parallel) faces which are coloured with that colour. The six possible paths of the hyper-ant correspond to the six different colours, i.e., each of them is “orthogonal” to the 4 squares of a fixed colour.

Regular polyhedra are polyhedra where vertices, edges and faces can not be distinguished. This requirement is so strong that there are only five regular polyhedra. At any rate, other polyhedra - although not regular - can strike us for their symmetry.

Here on the left you may see football and, below, a polyhedron with the same structure. It is not a regular polyhedron because the faces are not all equal - there are hexagons and pentagons. Yet, it does have a symmetry. The faces - although not all alike - are regular polygons. Moreover, if we look at a vertex, we realize that at each vertex there are a pentagon and two hexagons. We can imagine to make a plaster cast around a vertex and obtain a sort of three-dimensional "stamp", which can be adapted to any other vertex.

The football is an example of a uniform polyhedron, i.e., a polyhedron which has faces that are regular polygons and all vertices can not be "distinguished". This latter property allows one to identify the uniform polyhedra with numerical symbols, which represent the polygons adjacent to every vertex. For instance, (5,6,6) is the symbol of the football.
We could not use a symbol of this type for the polyhedron here on the right. Indeed, it has vertices with four triangles, others with two squares and two triangles, and others with three squares.

What do we mean by saying that the vertices can’t be distinguished? After all, vertices are points and,
undoubtedly, all points are equal! Already the example of the "three-dimensional stamp" tells us something about all the faces adjacent to a vertex and not only the vertex!

Actually, the problem is even subtler, and to say that the vertices can’t be distinguished, it is not even enough that a three-dimensional "stamp" adapts to any vertex with the same arrangement of faces.

The polyhedron on the right (the Miller polyhedron) has three squares and an equilateral triangle at every vertex; so a convenient three-dimensional "stamp" would adapt to any vertex. Yet, the vertices can be distinguished!
It is possible to see it by looking at the chain of squares that rounds the "equator" of the polyhedron. There is just one chain of this type because, if we start from other pairs of adjacent squares , we can’t make a full round. So, two vertices may be distinguished because they do not have the same position with respect to this chain like, for instance, the two vertices A and B.
It is impossible to move the polyhedron so that the vertex A maps to the vertex B and the polyhedron stays in the same position.

The other polyhedron you may see below "looks like" the Miller polyhedron quite a lot, but it is "more symmetric". There are three chains of squares and each vertex belongs to two of these three chains. With a little bit of patience, you may verify that the same three-dimensional "stamp" adapts to any vertex. Furthermore, for any two vertices there exists a symmetry of the polyhedron which maps the two vertices one onto the other. This is the requirement which must be fulfilled to talk about a uniform polyhedron (and to denote it by the symbol (3,4,4,4)).

Make a knot with a string and "fix" it by joining its ends. Next, let the string fall on a table: you get a "picture" of a curve which is almost flat. It is not totally flat - unless it is the unknot - because there are some points where the string does not lie on the surface of the table but it has some crossings.

You can represent this situation with a diagram where the discontinous piece of the curve stands for the branch of the knot that has an undercrossing.
This corresponds to project the knot on a plane, which results in a plane curve with some crossings. This curve is not enough to reconstruct the three-dimensional knot unless you specify every time the branch that goes above and the one that passes below.
Thus, the three-dimensional knot descends to a two-dimensional environment (a plane curve with some crossings and a specialization of over/under for each crossing). It is quite natural to imagine that the number of crossings of the curve can give some information about the complexity of the knot.

This is quite right; yet you need to be cautious. Indeed, the number of crossings may depend on the projection we choose, that is to say, how the string falls on the plane. It happens that a knot may seem to have three crossings under a given projection, and four from another view

.

There is even more to ponder! The investigation of knots is topological. This means that you do not have to think about knots like rigid objects.You can imagine that they are as long and extensible as you wish. You can also manipulate them in any way you want; so you obtain knots which can’t be distinguished from the original one as long as the knot stays tied. It is strictly forbidden to cut the string and tie it after making some operations on the knot. To summarize, you may have "legal" projections of the same knot where the number of crossings is much higher than the original one.

This is what happens for the knot represented by the exhibit from the exhibition matemilano. It is a trefoil as you may realize after you manipulate it for a bit.

In fact, when we speak about the “crossing number” of a knot, this does not mean (and could not mean!) the number of crossings of an arbitrary projection, but it refers to the MINIMUM number of crossings after ANY manipulation of the knot, followed by ANY possible projection on a plane.

It is not easy at all to compute this number. If you let a string fall on a plane and find out that the knot diagram has seven crossings, you need to be sure there is no other way of letting the string fall on the plane with a smaller number of crossings before you can say that the crossing number is indeed seven.

The crossing number of the unknot is 0. The crossing number of the trefoil is 3; there is no knot with crossing number 1 or 2. In fact, if you draw a knot with one or two crossings, you actually get the unknot, i.e., an object which can be manipulated into a circle.

The two trefoils ( right trefoil and left trefoil) are the only ones with crossing number 3. The figure eight knot is the only one with crossing number 4. The number of different possible knots with a given crossing number increases a lot as this crossing number gets higher: with nine crossings you have more or less one hundred possibilities!

The history of knot theory is very interesting. Some forerunners of this theory - P.G. Tait and W. Thomson (or Lord Kelvin) - began to investigate knots at the end of the XIXth century. Their study was based on a theory regarding the structure of matter, which appears very imaginative these days. According to this theory, the atoms (or vortex atoms) were not points but small knots which interlinked and formed molecules. With atoms in the back of their mind, Tait and Thomson aimed at classifying knots. Very likely, they undervalued the problem, which in fact has not been hitherto solved. The first "knot tables" date back to their trials, i.e., the first lists of knots which were ordered with respect to the crossing number.

In the compilation of these lists (with knots up to crossing number 10), Tait made some claims that he thought they were so obvious they did not need any proofs - such claims were related to the number of crossings. As time went by, the claims turned into conjectures - the so-called "Tait conjectures". They have been proved only in recent years in spite of the growing specialization of the techniques available in knot theory.