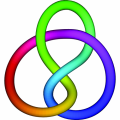
The torus knots are knots that can be drawn on the surface of a doughnut. The mathematical name of a doughnut is torus, and that is why they are called torus knots.

These knots are completely determined by a pair of integers, and it is not too difficult to understand how this works. One can form a torus by gluing together the edges of a cylinder, so let us try to generate the torus knots from a cylinder. Fix on the surface of a cylinder some number (three in the picture) of line segments parallel to the axis of the cylinder and uniformly spaced around the surface of the cylinder. In the example of three segments, each can be obtained from the other through a 120 degrees rotation, since 120=360/3.

Now, imagine that the cylinder is flexible and let us close it up so to give it the shape of a doughnut or torus.


In doing so, we have three points on each circle—the ends of the line segments—that have to be identified. If we glue the two circles without any twists, then each endpoint of one of the line segments on one circle is identified with the point on the second circle belonging to the same segment. The result is three circles that are not linked, which is not very interesting.

However, if we twist the cylinder before gluing together the edges, we have a number of interesting possibilities. Of course, we cannot twist arbitrarily. We must twist in such a way that each of the three endpoints of the segments on one circle is glued to one of the three endpoints on the second circle. The twist must therefore correspond to an angle that is a multiple of 120 degrees. This process explains why torus knots are characterized by two numbers: the (p,q) torus knot is obtained from p equally spaced segments on a cylinder whose endpoints are identified after the cylinder is twisted through an angle of q x (360/p)degrees.

The result of this process can be a knot with more than one component. Such cases can be easily read off from the two numbers. Indeed, the number of components is equal to g.c.d(p, q), that is, the greatest common divisor of p and q. In particular, we get a knot with a single component when p and q are coprime.

For instance, let p = 2. That is, let us begin with two line segments on a cylinder. We will obtain a one-component knot when q is odd, and a knot with two components when q is even.

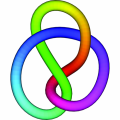
The (2,1) torus knot is the unknot. The (2,2) knot is made up of two linked circles. The (2,3) knot is the trefoil. The (2,4) knot is the Salomon knot, of which there are countless examples in art (since the time of stone engraving).The (2,5) knot is often used in artworks. One of the "imitators" of the Borromean rings is also a torus knot, namely the (3,3) knot.
The two integers that characterize a torus knot can be interpreted as representing the number of times that the curve (or curves) "winds around the hole". The number p gives a measure of how many times the curve winds longitudinally; that is, to obtain p, one can count the number of points in which the curve intersects a meridian. The number q gives a measure of how many times the curve winds in the other way; that is, to obtain q, one can count the number of points in which the curve intersects a parallel.

Torus knots are a family of knots which are "handy" to be investigated because they are completely determined by two integers. They are an example on which it is quite natural to test general statements on knots. This family is quite rich so that the examples are not trivial; at the same time, it is fairly convenient to be studied with respect to the intricacies of a generic knot

Look at the map of Milan which dates back to the XVI century. It is more or less a decagon, where the perimeter is represented by the Spanish Walls and the vertices are the Sforzesco Castle and the nine entrances to the city. How can we represent Milan from this map in a "science fiction" way so that the city extends to all the surface of a torus, or a double torus, or a Moebius strip?

To understand how we will proceed (clearly arbitrarily!), it is useful to keep in mind the video games where the cursor moves out of the screen and moves back in on the opposite side of the screen at the same height. For these video games, it is as if the proposed problem on the screen were actually proposed on the surface which is obtained by gluing the two edges where the cursor goes out and goes back in. The glueing pattern is given by the way in which the cursor goes back in.
For example, having a cursor that goes out on the right and goes back in on the left at the same height is equivalent to moving on the surface of a cylinder; Having a cursor that goes out on the right and goes back in on the left not at the same height, but "upside down" is equivalent to moving on the surface of a Moebius strip. The Moebius strip is the surface that can be obtained from a rectangle by glueing two opposite sides after giving to the rectangle a half-twist. Here "upside down" means that when the cursor goes out of the screen up on the left, it goes back in down on the right and vice versa.
If, finally, the cursor can not only go out on the left and go back in on the right (at the same height), but also go out from the top of the screen and go back in from the bottom of it (at the same distance from the vertical left side), it is as if we were on a torus.

For a cylinderand a Moebius strip the operations above can be concretely achieved with a sheet of paper (as long as it is long and narrow enough for the Moebius strip), for a torus paper is not enough. Paper is rigid
and it is possible to glue two sides of a rectangle so to make a cylinder. On the other hand, the cylinder can not be "bent" to glue the two boundary components. To make it, we need to imagine that our material is not paper but a sheet of elastic and deformable material. We can also trust virtual virtuale, animations or our imagination!

Let us go back to the map of Milan , and try to draw it on a Moebius strip, that is to say, describe how we made the model of the Moebius strip as an an exhibit of the exhibition matemilano. It is not a long and narrow rectangle whose opposite sides are to be glued. This is not a problem at all! From a topological point of view, we are allowed to perform any deformation we want. Therefore, we must decide which parts of the Spanish Walls should be identified. These are the parts which will not appear on the boundary of the strip. In the exhibit, the glued sides are those which start from the Castle and which correspond - in a modern map - to via Boccaccio on one side and to via Legnano/ bastioni di Porta Volta on the other side - but this has been completely random!

You can see what we did in the following pictures. In the first one we stretched the map. In the second one (which is somehow redundant) we cut and sewed the first picture following the identification scheme. Thus, we obtained a long and narrow rectangle and, from it, a Moebius strip. Here you see the final outcome.

There are other things to do. For instance, you can obtain a double torus as well. You just (!) need to start from the decagon given by the map of Milan and identify the edges like in this picture. It is not clear at all that we obtain a double torus: the sequence of pictures obtained following the links (starting from this one) is a nice "imagination exercise".

Let us compare a knot with that represented by its mirror image: is it the same knot?

In general, we can not move something onto its mirror image via a rigid motion - just think of a pair of left and right shoes - We will be tempted to say that the two knots are different.

On the other hand, we can perform various motions that move one knot to the other (and conclude that the two knots are the same). For instance, we can wind the string, stretch it a bit as if it were long as much as we want; we can move it in any way as long as we do not untie it. This wide spectrum of operations makes us think that the answer to our original question is positive: after all the two knots "look alike" quite a lot!

Actually, both answers are wrong for all knots. For some knots the answer is "yes" and for some others the answer is "no".

For instance, the figure eight knot is the same as its mirror image . This is easy to verify - just play with a string or follow the links from this image. On the other hand, a right trefoil can not be manipulated until it becomes its mirror image, which is called a left trefoil.

It is not so easy to prove the second claim. In fact, if we are able to manipulate a string till a knot becomes a different one, we are sure that the two knots represent the same one. If we are not able to, how can we say it is indeed impossible? How can we say that we were not able to and that someone else might have succeeded?

Mathematically speaking, to be certain that our claim does not hold, we associate a "mathematical object" with every knot. It could be a number or something even more complicated like, for instance, a polynomial. This object should be concretely and explicitly calculated from a particular position of a knot. For example, we could think of a diagram like one of those in this leaflet or of a string in three-dimensional space.

The value of this mathematical object may a priori change if we start from a different position of the knot. If, however, we can find some way to associate the knot with the object so that the value of this object does not change with respect to the operations which correspond to the real "manipulation" of the string, we come up with an "invariant" of the knot, i.e., something that depends only on the knot and not on a particular projection or a particular diagram.

If we find an invariant which takes two different values on two different knots, we can be certain that the two knots are really different, i.e., they can not be moved one onto the other.

This is exactly what happens for the right and the left trefoils.

How many uniform polyhedra are there, and what is their structure?

To begin with, there are five regular polyhedra.

Another standard example (more precisely a family of infinitely many examples) is given by prisms. A right prism with basis a regular polygon is a (4,4,...) uniform polyhedron as long as the height of the prism makes all the lateral faces squares.

There are infinitely many uniform polyhedra among prisms, one for every regular polygon which is fixed like its basis - in particular, if the basis is a square you get a cube). Here on the left you may see a (4,4,6).

There is another family of polyhedra (maybe less known), which contains infinitely many uniform polyhedra: it is the family of antiprisms. Here on the right you may see a uniform antiprism of type (3,3,3,5): each vertex is adjacent to three equilateral triangles and a pentagon.
It is easy to imagine how you can get a uniform polyhedron if you start from any regular polygon and not just from a pentagon. In particular, if the basis is an equilateral triangle, you get the octahedron).

Are there other uniform polyhedra in addition to prisms, antiprisms and regular polyhedra? How many and which ones? In fact there are some of them, but not too many: thirteen all together, which are sometimes called archimedean polyhedra. If we want to list them, as we did for the others, with a numerical symbol, the full list can be given in the following table:

The table has been made following a pattern which can be useful to describe the corresponding polyhedra. The polyhedra in the first column are related to the cube, those in the second are related with the dodecahedron and those in the third column with the tetrahedron.

Almost all the polyhedra in the first column have the same symmetry of the cube. They can be seen in a kaleidoscope, in particular that associated with the cube. Only the polyhedron on the last row has a symmetry which is similar to that of a cube, but differs from it because it contains only rotations - thus it can not be seen in a kaleidoscope.

Analogously, all the polyhedra in the second column - except the last one -, scan be seen in the kaleidoscope of the dodecahedron; those in the last column can be seen in the kaleidoscope of the tetrahedron.

The row layout is not random. For instance, the (3,8,8) polyhedron represented below can be obtained from a cube by "smoothing" the vertices so that one gets equilateral triangles and regular octagons.
The other two polyhedra in the same row of the (3,8,8) are obtained in the same way, but starting from a different polyhedron. To obtain a (3,10,10) one starts from a dodecahedron and to obtain a (3,6,6) one starts from a tetrahedron.
Something similar occurs for the other rows of the table.

People who like numerical patterns may have noticed that the symbols of the second column can be obtained from the corresponding ones of the first column by substituting some "4" in "5" and some "8" in "10". How can we explain this phenomenon? And why is only the central "4" in (3,4,4,4) exchanged with a "5" and not the other two "4"? If you observe the polyhedra that you find below, you may find an answer...