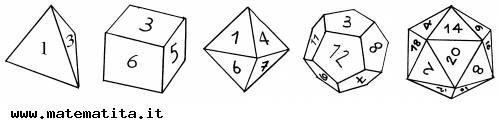
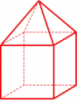
All of us agree on the fairness of using a cube, or indeed any of the regular polyhedra, to play dice, because any face has the same chance to appear. From a mathematical viewpoint, we say that the faces are indistinguishable. But what does "indistinguishable" mean exactly?

This adjective indicates that if we have a regular polyhedron and we choose two of its faces, we can always rotate it so that the first face goes to occupy the place of the second one and, as a whole, the polyhedron goes back onto itself.

For example, to move the front face of the cube in the figure to the position of the top face, it is enough to rotate the cube through 90 degrees about the straight line labelled r in the figure.

The same thing happens for two vertices or two edges:
to send edge a onto edge b we can rotate the cube through 120 degrees
about the straight line s; the same rotation can be used to send vertex P onto vertex Q.

The table below describes the five regular polyhedra.

In the table, the first three columns of numbers give the number of faces,
edges, and vertices for each polyhedron; the two following columns can be interpreted as the "instructions" to build the skeleton of the polyhedron if sticks of the same length together with something to connect their ends are available (for example some drinking straws with pipe-cleaners for making joints). So the numbers that appear in the last row tell us that in an icosahedron there are 20 faces, 30 edges, 12 vertices, 5 edges meeting at each vertex, and 3 edges per face: if we join straws five at each vertex and form triangular faces, the object will "close itself" and give rise to an icosahedron.

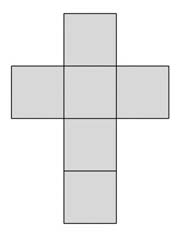
The last column in the table also gives instructions for building the corresponding polyhedron: in this case, starting from the drawing of the net on cardboard we can obtain the surface of the polyhedron, rather than just its skeleton.

There is other information that we can extract from the table.
For example, the fact that the cube and the octahedron are "relatives":
they have the same number of edges, and each of them has as many faces as the other has vertices.
Also, the number of edges meeting at any vertex of one is the same as the number of edges around a face of the other.
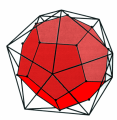
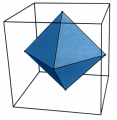
This relationship is made clearer in the figures on the left: if we consider the centres of the faces of a cube and we join two of them when the corresponding faces have an edge in common, we will obtain an octahedron.

And vice versa, if we perform the same procedure starting from an octahedron, we will obtain a cube.

Also the dodecahedron and the icosahedron are relatives, in the sense above, as we can notice both from the numbers in the table and the figures.

Now what is "relative" of the tetrahedron?
There are no more regular polyhedra, but the fact that the regular tetrahedron has as many faces as vertices may help you to find an answer.

There is a large variety of flowers whose petals are symmetrically arranged around the centre.
Let us look, for example, at the periwinkle shown on the left, and fix our attention on one of its petals: we can pass from this one to any other by rotating the flower about its centre in such a way that each petal reaches one of the five possible positions.

The periwinkle has only these five rotations as symmetries.

On the other hand, this other flower and also the one drawn here on the right has five reflections as well, reflections in each of the lines through the centre and the tip of a petal.

The pentagonal symmetry type is very common in the organic world: flowers apart, we can also find it in starfish and sea urchins. Apples and pears, too, have pentagonal symmetry: to see this, H.S.M. Coxeter suggests cutting an apple in the way you would cut an orange to squeeze out its juice, and look at its core.
Nature offers many examples of shapes that display a similar symmetry based on other numbers. For example, there are six rotations that transform a snow crystal into itself (and six reflections too), while there are three rotations (and three reflections) that transform a slice of banana or a courgette flower into itself.

In art there are extraordinary examples of buildings and patterns that are symmetrically arranged about a centre: the circular Pantheon in Rome, the octagonal Baptistry of the Cathedral in Florence, rose windows of Romanesque and Gothic churches, some mazes, Aztec calendars, and Indian mandalas.
A design is called a rosette if its symmetries are either only rotations or an equal number of rotations and reflections. In fact, it is not possible for a design to have different numbers of rotational and reflection symmetries. It appears that this conclusion was reached by Leonardo da Vinci when he was trying to determine all the possible symmetries of a building with a central plan.

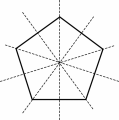
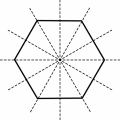From the mathematical point of view, the simplest rosettes are the regular polygons, that is those polygons with equal edges and equal angles. The snow crystals, for example, are nothing but magnificent elaborations of a single fundamental theme, the regular hexagon.

Would you like to make a paper model of a rosette?
Take a sheet of paper, fold it so that all the creases pass through the same point, and cut out a profile: by unfolding the paper you will have a rosette.
Note a rosette made in this way will always have both rotational and reflection symmetries.
Can you make one with only rotational symmetries?

by Paola Cereda
Transalated by Elisabetta Beltrami and Peter Cromwell

If we unfold a hypercube, should the cubes not disappear upon making the identifications?

The six squares in a net of the cube are the six faces of the cube and the eight cubes in a net of the hypercube represent the “cubic faces” of the hypercube. In other words, the eight cubes represent the “exterior” of the hypercube, that is to say, what you should “see” of the hypercube in four-dimensional space.

On the other hand, if we imagine to glue the faces of the cubes two by two (as required by a net) , the faces should not be visible any more and not even the cubes! But if you can not see the eight cubes, where is the hypercube?

This time, the analogy is extremely difficult since we must study not only the three-dimensional analogue, but we must also suppose that we are “two-dimensional” observers. More specifically, we must imagine that we are two-dimensional beings who live on a plane where you find two squares, each of them with three black edges and one red edge.

Now, let us suppose that the two squares are glued red edge by red edge. We should see the exterior of a rectangle with four black edges; the red edge would disappear from our sight! But if you raise your head from the plane, you can still see the red edge.

Likewise, if two cubes have a face in common in four-dimensional space, you can still see this face (it is “external”). In particular, you can still see each face of the eight cubes in four-dimensional space although they are glued face by face.

Many everyday objects have bilateral symmetry: furnishings, lamps, road signs, flags, musical instruments and some of our clothes (but not individual gloves, or shoes). So do many animals and leaves; even the human body in its external form has approximate bilateral symmetry (though it would be different if we considered the internal organs too).


What does the phrase "this butterfly has bilateral symmetry" or "this butterfly has a plane of symmetry" mean?

Imagine cutting something in half along a plane and putting a mirror in place of this plane. If the reflected image together with the original half reconstructs the whole object then the plane is a mirror plane or plane of reflection symmetry.

In practice, it can be rather hard to cut a fork in half, not to mention a butterfly or a human being (even if the imagination of Italo Calvino tried it in the novel "The Cloven Viscount"). It is easier to do analogous experiments with planar figures, in which case mirror symmetry is no longer defined by a plane, but by a straight line.

To check whether a particular straight line is a line of reflection symmetry (mirror line) of a figure, we can place a mirror along the line and hold it perpendicular to the plane of the figure. For the line to be a mirror line, the reflected image together with half the original must reconstruct the whole object. As you can see from the two figures below, this need not happen, even if the straight line divides the figure into equal parts.

What happens when we use two mirrors?
Suppose, for example that we place a "p" between two parallel mirrors: then you can see a series of images which repeat along a strip, alternating images of "p" with images of "q".

If we make first a reflection with respect to a straight line, and then another reflection with respect to another line parallel to the first one, the combined effect is equivalent to that of a traslation, in the direction perpendicular to the two mirror lines, and of a distance twice the distance between the two mirrors.

A reflection exchanges the right with the left: in fact the mirror image of a "p", which has a tail on the left-hand side, is a "q", with a tail on the right. A translation, instead, corrisponds to two reflections and so ... the tail of the "p" comes back to its place!

What happens if the mirror lines are not parallel but meet?




Placing an object between two connected mirrors (as shown in the figure, a cat with its tail on the right), you can see some images of the object, and, among these, those with the tail on the left alternate with those with the tail on the right. The images are no longer positioned along a strip, but around a centre, instead. In effect, if we make first a reflection with respect to a straight line, and then another reflection with respect to another line which has a point in common with the first one, the effect obtained is equivalent to a rotation about this point, by an angle twice the angle between the mirror lines.

How many images are seen?

If the angle between the mirrors is a submultiple of 180 degrees, as in the figure here (where the angle is 60 degrees) then the 360 degree angle is divided by the mirrors - both real and virtual ones - into an even number of angles (six in the figure) each of which contains an image: half of them (three in the figure) contain an image obtained from the original object by rotation (and so the cat has its tail on the right), while the others are obtained from the original object by reflection (and so the cat has its tail on the left).

When we throw a die we expect, since its shape is evidently symmetric, that any of the six numbers marked on its faces has the same probability to appear.

In some toy shops, besides the usual six-faced dice, you can also buy dice with four, eight, twelve e twenty faces.

What is special about the five polyhedra represented by these dice? To see what properties they have, we first consider some other examples of polyhedra.

We could build a die from a geoid, for example. Such a polyhedron could even seem more "regular" than the five dice above since its shape is "closer" to that of a sphere, but, if we study it carefully, we notice that its vertices are not all of the same type: at some vertices (like A) five edges radiate and so five triangles come together; at others (like B) six edges start and so six triangles meet.

We call a polyhedron regular if all its faces are equal regular polygons and the same number of faces meet at every vertex. In such a polyhedron all the faces, edges and vertices are indistinguishable.

None of the polyhedra in the second figure above is regular, while the five dice are all examples of regular polyhedra. Are there any more? (After all, in the plane we can build regular polygons with as many edges as we like.) The answer is: no. In space, there are only the five regular polyhedra of the diceshown in the first figure.

Even the ancient Greeks knew this fact; it so impressed them that the Pythagoreans, and later Plato, built their cosmogonical theories on it, associating the fundamental constituents of nature to the five regular polyhedra. Because of this, the regular polyhedra are also called Platonic solids.

In his `Timaeus', Plato describes the tetrahedron as "element and germ" of fire, the octahedron of air, the icosahedron of water, the cube of earth, and the dodecahedron represents the image of the entire universe: "There still remained a fifth construction, which the god used for embroidering the constellations on the whole heaven".
The last book of the Euclid's "Elements" is dedicated to the five Platonic solids, to some of their properties and relationships, and to the proof that there are no other regular polyhedra.

Models of regular polyhedra have been found from pre-Greek civilisations. The harmony of their proportions and their mathematical properties give them a charm that has been captivating artists and scientists ever since.
Dodecahedra had a religious meaning in the Etruscan civilisation, and were also used as dice by the Romans.
In the Renaissance, regular polyhedra were used as a good subject for studies of perspective: we can find them in works by Paolo Uccello, Piero della Francesca, Albrecht Dürer, Leonardo da Vinci, Luca Pacioli and Leonardo Pisano (also known as Fibonacci).

In 1595 Kepler believed that he had "penetrated the secrets of the Creator" because he had elaborated a model of a planetary system (that later became discredited) by using the Platonic solids to describe the distances between the elliptic orbits of the six planets then known.

Shapes inspired by regular polyhedra are also common in modern art and design, from works of Escher to modular architecture, to objects by Munari.
One last curiosity: in France they built dodecahedral bottle banks.

Even nature shows us examples of regular polyhedra: some cristals , viruses which often have icosahedral form, simple living organisms like radiolaria, ...