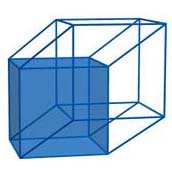
A net, a Schlegel diagram or a perspective projection: which of these three methods best represents a hypercube? The answer is: “ It depends”. In fact, they are three-dimensional representations of a hypercube, but they are not the hypercube. A representation may be more fit to study a property than the others.

For example, a Schlegel diagram seems to be the best for some combinatorial problems. On the other hand, it is more appropriate to choose a net for some optimization problems, such as finding the shortest path between two points. And yet, a projection shows more clearly that a hypercube contains infinitely many cubes. Having more than one representation allows one to get more information on the hypercube and its properties.

In other words, we do not take into account the hypercube, but we study an (easier) picture of it from which we infer some properties of the hypercube.

Likewise, mathematicians have defined various “representations” of four-dimensional space, which are very diverse (algebraic, analytic….). They are more or less complicated and difficult to work with, but they allow mathematicians to observe and describe various characteristics of four-dimensional space.

As recalled before, a net, a Schlegel diagram and a projection are three-dimensional objects; however, it is worth mentioning that a net is the only one that differs from the other two because a Schlegel diagram is essentially a projection. If we identify the faces of a hypercube as required, we get a real hypercube. Actually, we can not do it in practice because our space is three-dimensional. It is a widely common technique in Topology to make up objects of higher dimension via identification of faces, segments, points, namely objects of smaller dimension. This technique allows one to make a great deal of diverse objects from simpler shapes.

For example, consider a square and identify the two pairs of opposite edges. If you assume the square be flexible and deformable, you can make these identifications in three-dimensional space: you will get a doughnut.

If you give a half-twist in one of the two identifications before you glue a pair of opposite edges (so as to change their direction), not only is the doughnut unobtainable, but it is actually not feasible to deform a square in three-dimensional space without forming any self-intersections. On the other hand, it is possible to make these identifications in four-dimensional space. This object is known as the Klein bottle.

The photograph above shows the blue kaleidoscope, in which a
virtual cube can be produced, with a single ball placed in it.
The arrangement of the reflected images of the ball helps us to discover
the angles between pairs of mirrors of the kaleidoscope: there are some rings of four balls, and each of these corresponds to a pair of mirrors that meet at a right angle; there are some rings of six balls, corresponding to mirrors meeting at 60 degrees; finally, there are some rings of eight balls, which correspond to mirrors that meet at 45 degrees.

We can recover these angles if we consider the sphere corresponding to the kaleidoscope.The surface of the sphere is divided into 48 "triangles", all equal to each other, whose angles are 90, 60 and 45 degrees - in fact there are vertices surrounded by four triangles (hence each of the four angles meeting there is 90=360/4 degrees), vertices surrounded by six triangles, and vertices surrounded by eight triangles.

But 90+60+45 is 195, and not 180, so we have a triangle whose angles do not add up to 180 degrees! We should not be too surprised at this fact, because we are not really dealing with a proper triangle: it is a "fat" triangle, drawn on a sphere, whose edges are not straight lines, but the nearest thing that can be drawn on a sphere, that is arcs of great circles.

What kind of geometry applies to triangles on a sphere? What does it have in common with, and how does it differ from, the usual plane geometry that we are familiar with? We have just seen one difference: the sum of the angles of a triangle is no longer 180 degrees.
Moreover, the angle sum is not even the same for all triangles: by examining the spheres corresponding to the other two kaleidoscopes, we can see that one sphere is divided into 24 triangles, all equal, each of which has one angle of 90 degrees and two of 60, while the other sphere is divided into 120 equal triangles, each of which has an angle of 90 degrees, one of 60, and one of 36. The sum of the angles in the first case is 210 degrees, in the second case it is 186 degrees.

The situation is summarised in the table above: the first column contains the sum of the angles of the triangle; the second column, the angular excess (that is by how much this sum exceeds 180 degrees); the third column, the area of the triangle as a fraction of the area of the sphere.

We can see that the larger the triangle, the larger is the sum of its angles.
For the triangles of the sphere corresponding to the red kaleidoscope, which are the smallest ones (their area is 1/120 of the area of the sphere), the angular excess is only 6 degrees.
For the triangles of the sphere corresponding to the blu kaleidoscope, which are larger (their area is 1/48 of the area of the sphere), the angular excess is 15 degrees.
Lastly, we have the triangles on the sphere corresponding to the yellow kaleidoscope: notice that each triangle is formed by two of the triangles on the "blue" sphere so the area is doubled; this time the angular excess is 30 degrees. So we see that doubling the area of a triangle also doubles its angular excess.

This is not a special case. One of the characteristics of the geometry on the sphere which distinguishes it from the usual geometry on the plane is the fact that similitude does not exist: that is we cannot - as on the plane - draw two figures with the same shape but of different sizes.
The size affects the shape, and vice versa: we cannot find a spherical triangle larger than the one shown here in the figure which also has the same angles.
Of course, we could start from a larger sphere, but if the angles are of 90, 60 and 45 degrees, the area of the triangle will still be 1/48 of the area of the sphere. In fact, the area of a spherical triangle is proportional to its angular excess.

Are there also "thin" triangles besides "fat" ones? That is, are there triangles for which the sum of their angles is less than 180 degrees? The answer is yes, and the corresponding geometry is called hyperbolic geometry. The figure to the right (which recalls the structure of some drawings by Escher) is a companion of the spheres corresponding to the kaleidoscopes (and of the grids corresponding to the planar triangles): here too there are some "triangles" (thin ones), all equal to each other, and this time the angles are of 90, 60 and 360/14 degrees.

The interesting thing is that this situation is totally "symmetric" with respect to what we have seen before for the geometry on the sphere: again, in hyperbolic geometry, there is no similitude; the sum of the angles of a triangle is alway less than 180 degrees; the shape of a triangle determines its size; the area of a triangle is proportional to its angular defect, that is to how much the sum of its angles is less than 180 degrees. But this is just the beginning of a long story ...

A net of the hypercube allows us to represent the hypercube in three-dimensional space, but it is not the hypercube. We can wonder where the fourth dimension is “hidden” and how it is possible to make up – with some cubes – a four-dimensional object like a hypercube. In fact, the eight cubes, that we see, represent the exterior of the hypercube; yet, the fourth dimension “lies” in the interior of the hypercube……

The word "wallpaper pattern" in mathematics indicates a plane figure whose symmetry group (that is the set of all those transformations of the plane that leave distances unchanged and map the figure onto itself) is discrete and contains some translations. These translations don't point in just one direction, as occurs for friezes, but in at least two different directions.

It is possible to prove that for wallpaper patterns there are 17 distinct symmetry groups (and seventeen only!).

Among them:

• Two groups contain rotations in 60° multiples (60°, 120°, 180°,240°, and 300°, and the identity):
  
  

  	632(p6) contains translations and rotations only (60° and multiple)
  	*632(p6m) contains reflections too.

  
  
  
• Three of them contain rotations in 90° multiples (90°, 180°, 270° and the identity):
  
  

  	442(p4) contains translations and rotations only (90° and multiples).
  	*442(p4m) contains reflections whose lines are pointing in four different directions.
  	4*2(p4g) contains reflections whose lines are pointing in two different directions.

  
  
  
• Three of them contain rotations in 120° multiples (120° and 240°, and the identity):
  
  

  	333(p3) contains translations and rotations only (in 120° multiples).
  	*333(p3m1) contains reflections too; all centres of rotation belong to an axis of symmetry of the figure.
  	3*3(p31m) contains reflections too; there are rotation centres that do not belong to an axis of symmetry of the figure.

  
  
  
• Five of them contain 180° rotations only (in addition to identity):
  
  

  	2222(p2) contains translations and rotations only (in 180&° multiples).
  	*2222(pmm) contains reflections whose lines point two different directions; all rotation centres belong to an axis of symmetry of the figure.
  	2*22(cmm) contains reflections whose lines point in two different directions; there are rotation centres that do not belong to an axis of symmetry of the figure.
  	22*(pmg) contains reflections whose lines point in one direction only.
  	22×(pgg) does not contain reflections; it contains glide-reflections (that is the composition of a translation and a reflection, whose axes is parallel to the translation vector).

  
  
  
• Four of them do not contain rotations (apart from the 360°, rotation [the identity] which belongs to the symmetry group of all figures):
  
  

  	o(p1) contains translations only.
  	**(pm) contains reflections; it does not contain glide-reflections, apart from the "mandatory ones", that result from the composition of the reflection in an axis of symmetry of the figure, with a parallel translation.
  	*×(cm) contains reflections too; it also contains glide-reflections, whose lines are parallel to axes of symmetry, but that in turn are not axes of symmetry of the figure.
  	××(pg) does not contain reflections; it contains glide-reflections.

In this description we have not indicated all the transformations that one can find in each group, nor have we written each characteristic and property, but we have provided enough to distinguish each one of the 17 groups.

You can find some interactive animations about wallpaper patterns in Draw your own wallpaper pattern and Recognize a wallpaper pattern.

In mathematics the word "rosette" indicates a plane figure whose symmetry group (that is the set of all those transformations of the plane that leave distances unchanged and map the figure onto itself) contains only a finite number of transformations.

It can be proven that the only two possibilities for a rosette's symmetry group are cyclic groups (that are denoted with the symbol Cn and that contain n rotations) or dihedral (that are denoted with the symbol Dn and that contain n rotations and n reflections).

For any given integer number n, there is a corresponding cyclic group Cn and a corresponding dihedral group Dn.

cyclic groups		dihedral group
C1	C2	D1	D2
C3	C4	D3	D4
C5	C6	D5	D6
C7	C8	D7	D8
...	...	...	...