The orbifold shop and Conway’s “magic theorem”: the case of wallpaper groups

A nice interpretation (due to Conway) of the analysis of the different cases corresponding to wallpaper groups is the following: let’s imagine a shop selling all the different components we just described, that is the various parts which constitute an orbifold: conical points, corner points, mirror lines (corresponding to a star *), miracles (corresponding to a cross ×) and wonder-rings (corresponding to a dot o). Each one of these components has a cost and the price list is the following:

• a dot ο costs 2 Euros
• a cross × costs 1 Euro
• a star * costs 1 Euro
• a conical point n of order n costs (n-1)/n
• a corner point n of order n costs (n-1)/2n.

The “magic theorem” (so called by Conway) states then that a plane orbifold (corresponding to a wallpaper group) costs exactly 2 Euros, and that any combination of symbols costing exactly 2 Euros gives rise to a plane orbifold. Then, we can discover with a bit of patience all the possible mixing of dots, crosses, stars, conical points and corner points giving a total cost of 2 Euros, and we find, as a corollary of the magic theorem, that there are exactly 17 possible cases; precisely they are:

ο	2222	333	442	632
	*2222	*333	*442	*632
	2*22	22*	3*3	4*2
	**	*×	××	22×

The orbifold shop and Conway’s “magic theorem”: the case of friezes

Dealing with friezes, we have a new symbol (∞) in the signature, costing 1 Euro if it appears before any star *, and costing 50 cents if it appears after a star; this choice is consistent with the fact that the limit of
(n-1)/n, when n tends to infinity, is 1, while the limit of (n-1)/2n, when n tends to infinity, is 1/2. Thus, we can imagine it associated to a “center of infinite order”, corresponding now to a translation instead of a rotation. The magic theorem for friezes asserts then that we get a plane orbifold corresponding to a frieze if and only if the total cost is exactly 2 Euros and the signature contains at least one symbol ∞. Here also, with a bit of patience, one can list all the possibilities, and there are 7 of them:

∞∞

22∞

∞×

∞*

*∞∞

2*∞

22∞

The orbifold shop and Conway’s “magic theorem”: the case of finite groups of space isometries

We said that Conway’s notation works also for all possible symmetry types corresponding to finite groups of space isometries (and the quotients are the so called elliptic orbifolds). In this case, when we speak of a quotient, we are referring to the quotient of a sphere (not of the whole 3d space) with respect to the group. In order to understand where this sphere comes from, let’s begin with the example of a cube (which is here the analogous of the drawing in the plane case). The symmetry group of the cube consists of all space isometries sending the cube to itself. All these isometries fix the same point, the center of the cube; thus, they fix also any sphere with center in this point. 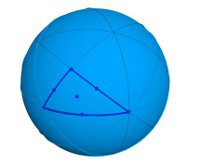On the sphere we see here (and that we should imagine with center in the center of the cube) we see a slightly different colour to mark different parts corresponding to the faces of the cube (as if a blue cube, with faces a bit darker or lighter, had been blown up to a sphere); the lines we see are great circles on the sphere and they correspond to the intersection of the sphere with the (9) symmetry planes of the cube; the triangles are the projections on the sphere of the 48 (=6×8) triangles that we obtain on the cube if we cut it with its symmetry planes all together. When we speak of an orbifold in a situation like the symmetry group of the cube, we refer just to the quotient of this sphere with respect to the group: thus, in order to get the orbifold, we do on the sphere the same operations we did in the first examples starting from the plane: that is, we have to identify all the points of the sphere which lie in the same orbit with respect to the symmetry group of the cube. For example, a point where 4 great circles meet corresponds to the center of a face in the cube, and all these points are “the same” (meaning that one of these points is enough to represent them all in the quotient), because, for any two faces in the cube, we may find an element of the symmetry group of the cube (fixing the cube and) sending one of the two faces into the other one. Similarly, a point where 3 great circles meet corresponds to a vertex of the cube, and all the 8 vertices lie in the same orbit, thus giving one single point in the quotient; lastly, a point where two great circles meet corresponds to the midpoint of an edge of the cube, and all these points also are in the same orbit. The quotient is a spherical triangle (with angles 90°, 60° and 45°), and we can describe this orbifold, like we did for plane orbifolds, with the Conway signature *432. If we then calculate the total cost of this orbifold, we get 1 + 3/8 + 2/6 + 1/4 = 1 + 23/24 <2. This is not a coincidence. In fact, the magic theorem asserts in these cases that in order to get one of these orbifolds (which are named elliptic orbifolds, and are the quotients of a sphere with respect to a finite group of isometries) it is necessary that the total cost is less than 2 Euros. The different possibilities we get for building a Conway signature with total cost less than 2 Euros include 7 different cases which are:

332

432

532

*332

*432

*532

3*2

but also some infinite families (depending on a natural number n):

n

nk

n×

n*

*n

*nk

2*n

22n

For plane orbifolds, the total cost equal to 2 Euros was both a necessary and a sufficient condition for the existence of the corresponding orbifold. Instead, for elliptic orbifolds, the situation is not exactly the same: in fact, there are 4 cases which have to be excluded because they do not give rise to an orbifold. They are:

n

*n

nk(when n≠k)

*nk(when n≠k)

So we are left with 7 infinite families:

nn

22n

n×

n*

*nn

2*n

*22n

Maybe some of you noticed the analogy between these 7 families and the 7 frieze groups; not only the numbers are the same and we get 7 possibilities in both situations, but, if we examine the list of the 7 Conway signatures in both cases, we realize that we can pass from one to the other one simply by substituting a n” with a “∞”:

∞∞

22∞

∞×

∞*

*∞∞

2*∞

*22∞

Of course, this is not a coincidence and there are also some decorations illustrating very well the reason of this analogy. Starting from a frieze, we can imagine to roll it up on a cylinder in such a way that the translation (which was sending any element to the “next” one) becomes now a rotation. Sometimes, we even give for granted, without realizing it, this analogy, for example when we very naturally call “frieze” a motif decorating (for example) the cylindrical apsis of a church (thus surely not a planar decoration!); we see it as a frieze, simply because we automatically imagine the same decoration spread out on the facade. 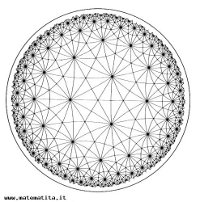Completely different (and much more various and rich) is the situation corresponding to (hyperbolic) orbifolds with a total cost greater than 2 Euros; in this case we can’t list all the possibilities, because they are infinitely many: here we see an example with Conway’s signature *237 (which has in fact a total cost of 1 + 1/4 +2/6 + 6/14 = 1+85/84 ›2).

The signature introduced by Conway to denote symmetry groups describes precisely their quotients, that is the orbifolds which act as stamps. This signature is a string containing numbers and symbols (a dot o, a star *, a cross ×; in the case of friezes, we have also the symbol ∞). Let’s see what these numbers and symbols mean.

• A number appearing before possible stars denotes in the stamp the vertex of a cone (we call it conical point) and the number gives the information about the opening of this cone (more precisely, the number k corresponds to an opening of 2π/k); on a plane drawing with that symmetry group, the number k indicates there exist symmetry centers of order k (that is: points P such that a rotation with center P and angle 2π/k sends the drawing to itself); moreover, the fact that in the string the number k comes before any star means that the corresponding rotations center in the drawing does NOT lie on a symmetry axis (and we call them gyration points); for example this image corresponds to a 3 in the string, while the centers of the black squares in this drawing give rise to a 4 in the Conway signature (because a 90° rotation with center one of these points leaves the drawing unaltered and the symmetry axis of the drawing do not contain these points).
  
• A star * indicates the presence in the quotient of a boundary line; on the plane drawing with that symmetry group, a star means there exist symmetry axis in the drawing (that is: lines such that the reflection with respect to that line sends the drawing to itself). It should not appear strange that a symmetry axis in the drawing gives rise to a boundary line in the quotient: let’s imagine a drawing like this one, with a very simple symmetry group containing, besides the identity, only the reflection with respect to a line; in order to construct the quotient, we simply have to “fold” the plane in half, following this line, thus getting a boundary line just corresponding to the symmetry axis. So, this drawing has in its Conway signature ** two stars; and the stars are two because there are symmetry axis of two different kinds: one passing by the paws of the birds, and a different one passing by their wings; and, also when we imagine the drawing repeating at infinity, all other symmetry axes may be sent in one of these two by a translation fixing the whole drawing.
  
• A number following a star * represents on the orbifold a corner point in the boundary line (and the number k means it is a corner with angle π/k); on a plane drawing with that symmetry group, a star followed by a number k indicates there are two symmetry axes meeting in a point P and making in this point an angle π/k (which means also that point P is a symmetry center of order k in the drawing). In the example of the mirror box corresponding to this drawing, the Conway signature is *442. Indeed, the quotient is just the triangle corresponding to the mirror box, and this has just one border line, with three angles measuring respectively π/4, π/4 and π/2. We can “read” on the drawing the fact we have two symbols “4” in the signature and just one “2” observing that all rotation centers of order 2 are equivalent (meaning that we can find a symmetry of the drawing sending one of them into the other one), while the rotation centers of order 4 are of two different kind (the centers of the small squares and the centers of the big ones).
  
• A cross × corresponds in the orbifold to attaching a Moebius strip; on a plane drawing with that symmetry group, the cross indicates what is called by Conway a miracle, that is the presence of two images, mirror images one of the other, such that we can find a path in the plane going from one to the other and NOT crossing any symmetry axis of the drawing: like we can see for example with the sequence of footprints in a regular walking. A wallpaper pattern having a cross in its Conway signature is the one we can see in a herringbone pattern: the corresponding group has Conway signature 22×.
• A dot o corresponds in the orbifold to the attaching of a handle; on a plane drawing with that symmetry group, the dot indicates the presence of what is called by Conway a wonder-ring, that is a couple of paths connecting three images which are related by translations (fixing the whole drawing), and such that there are no other ways to relate these images (through rotations or other isometries fixing the whole drawing); this is what we see for example in this drawing; this is also the only possibility for a wallpaper pattern whose Conway signature contains a dot (and, in fact, its Conway signature is just a single dot o).

Let’s see some other examples. Among the mirror boxes we find, besides the isosceles right-angled triangle, also an equilateral triangle corresponding to Conway signature *333, a right-angled triangle with angles 30° and 60°, corresponding to Conway signature *632 and a rectangle, with Conway signature *2222. We can observe that in the first case the order 3 rotation centers are of three different kinds (in this drawing, at the centers of the orange hexagons, at the centers of the pale blue ones, and of the dark blue ones): we call them “different” because we can’t find an isometry fixing the whole drawing and sending, for example, the center of an orange hexagon into the center of a pale blue one. On the contrary, in the second case all centers of order 3 are at the center of a blue hexagon and they are all equivalent (so they correspond to just one point in the quotient and just one 3 in the Conway signature), because they are in the same orbit, that is we can find an isometry fixing the whole drawing and sending any one of them in any other one; and similarly all the order 6 centers are equivalent (in the center of the stars) and also all the order 2 centers (in the points where two different stars meet), so that there is just one 6 and one 2 in the Conway signature. A situation like the one of this floor is an example where there are no symmetry axes, so no stars in the Conway signature, which is simply a 632 because we can find rotation centers of order 6 (all equivalent one another), of order 3 (all equivalent one another) and of order 2 (all equivalent one another). We find other cases analogous to this one corresponding to Conway signatures 442, 333, and 2222. There are also situations where we have together both some numbers preceding a star and some following it, and this illustrates very well the difference between these two cases: for example, in this drawing we already met, the wallpaper pattern has a Conway signature 4*2; in fact the rotation centers of order 4 (at the center of the black squares) do not lie on a symmetry axis, while the rotation centers of order 2 (at the center of the blue octagons) appear as the intersection points of two orthogonal symmetry axis. This kind of notation for the orbifolds can be used not only with groups corresponding to wallpaper patterns, but also with friezes (provided we introduce a new symbol, ∞), with finite symmetry groups of 3-dimensional objects, and also for some more complicated cases.

From the point of view of symmetry, when we look at a plane drawing, or at a 3d object, the algebraic structure which charachterizes it is its symmetry group, that is the set of all the isometries (plane isometries, or isometries of 3d space) which leave the plane drawing (or, respectively, the 3d object) unaltered.
Let us start, for example, from a drawing which repeats in the plane through a translation (like this, which we should imagine repeating at infinity both right and left); its symmetry group contains just translations: of 1 step, 2 steps, …, n steps, … , but also 0 steps (corresponding to staying still), or 1 step in the opposite direction, … or m steps in the opposite direction.
Let us imagine now to identify, as if they were just one point, all the points which are obtained one from the other through an element of the group (in mathematics this set of points is called an orbit and it is from this word that originates the word orbifold, which stands for orbit manifold.
If we fix (for example) the point corresponding to the tip of the big toe of a given foot, then the translation by one step sends this point to the tip of the big toe of the following foot, … and the translation by seven steps sends it to the tip of the big toe of the foot which is placed seven steps further away, and so on.
So, identifying to just one point all the points of the orbit means that we have just one point corresponding to the tip of the big toe, which is there to represent all the points which correspond to the tip of a big toe in any one of the feet.

Of course, we must do this not only for the point at the tip of the big toe, but for any other point, for the other toes, and for a particular point in the heel, etc; in order to understand what we get at the end of this process, we can place a part of the plane containing just one foot, for example a vertical strip that is one step large, and we can observe that all the points in the interior of this strip will not be identified (we don’t find a translation of one or more steps sending one into the other), while we should still identify the two vertical lines bounding the strip, which are obtained one from the other one just with a one-step translation.
Thus, we get a cylinder and this cylinder represents the quotient of the plane with respect to the symmetry group of the drawing (sometimes we will call it the quotient of the drawing, referring to the motif – here it is just one foot – which is drawn on the cylinder). Also for these drawings the quotient is a cylinder.
The interesting point is that we can imagine this cylinder as a “stamp” (just like a painting cylinder) which, when decorated with a certain motif, can reproduce on the plane the drawing we started from.

And this is exactly what makes the quotient a “significant” point of view: it is the (mathematical) object which contains, concentrated, all the informations we need in order to reconstruct the drawing we started from.
Also when we start from the drawing of the footprints in a normal walking, if we want to find the quotient, we get to detect a strip in the plane, which is bounded by two parallel lines: this time, however, in order to send a strip (containing for example just a right footprint) to the next one (containing a left footprint) we don’t need a translation but a glide reflection. Thus, as before, the two parallel lines bounding the strip are identified, but now they are identified “the opposite way round”: the result is not a cylinder any more, but it is a Moebius strip.

Let’s see another example. If we put some tiles in a mirror box we see a drawing and we can study its symmetry group; in order to understand the quotient of the plane with respect to this group, let us consider a point, for example the center of one of the small green squares: this point will be identified in the quotient with all the centers of all the green small squares (because, for any couple of green small squares, we can find an isometry which does not change the global drawing and sends the two squares – so also their centers – one to the other). However, the center of a green square will not be identified, for example, to the center of one of the big orange squares (because there does not exist an isometry fixing the drawing and sending one of these two points to the other one). If we move our attention to a vertex of the small green square, we discover that a rotation of 90° around the center of the square (which is an isometry sending the global drawing to itself!) sends this point to a different vertex of the same square (and, by iterating the same rotation, we can send it in each one of these vertices); this means that in the quotient we have a single point representing all the 4 vertices of all the green small squares.

Finally, the quotient is just the triangle corresponding to the mirror box and also this, just like the painting cylinder, acts as a “stamp” which can reproduce a drawing on the plane with the given symmetry group: the “motif”, corresponding to the drawing to be painted on the painting cylinder, is given now by the tiles we insert into the mirror box.

A last example: an image like this one has a much simpler symmetry group: the only isometries fixing the drawing are the 4 rotations with center in the same point, at the center of the drawing, and angles respectively 90°, 180°, 270° e 360° (the last one being the rotation of 0°, that is the identity, fixing everything). What is the quotient? It is enough to consider a sector of 90°, with vertex in the center of the drawing, and identify the two half-lines which are the boundary of this sector, thus getting a cone.

It is easy to imagine other examples similar to this one: the situation is nearly the same for the symmetry group of this drawing except that the angle corresponding to the “opening” of the cone is now 120° instead of 90°; while in this other drawing we have a narrower cone, corresponding to an angle of 45°. These cones also can be imagined as a stamp: if we decorate them with a motif, we can imagine to use them in order to reproduce on the plane a drawing which repeats the motif drawn on the cone for a certain number of times, depending on the angle of the cone: if we use the same cone and we change the motif drawn on it, we get different drawings with the same symmetry group.

The 17 wallpaper groups are an example of a (mathematical) situation where there exists a whole range of different notations (we may arrive even to 6 or 7 different notations!).

In this website, we have been using two different notations: initially the cristallographic one (p6, p6m, p4, p4m, p4g, …) and later, while keeping this one for people who are acquainted with it, we also began to use the Conway notation (632, *632, 442, *442, 4*2;…), which is the one we are going to explain here.

It would be nice if this notation (which has been introduced relatively recently by Thurston and Conway) could replace all the other ones in the next future!
This may happen, as in fact it is not just a notation which gives different names to the same objects, but it is rather a different point of view, which brings many advantages since it unifies situations which seem very different, thus managing to use the same kind of notation for wallpaper groups, but also for friezes and for finite groups of space isometries (that is, for example, symmetry groups of polyhedra).

The point of view we are referring to is the one of quotients which we can relate to Thurston’s “commandment” that is: “thou shalt know no geometrical group save by understanding its orbifold&&”.. You can find this commandment in the beautiful book by Conway The symmetries of things, in the introduction to the second part; the same book has been defined as “a testament to the power of good notation”.

This is the text of the poster you can see here.

When 2+2 is equal to 1

In common language, all things related to numbers are often used as models of unarguable certainty. After all, numbers are used to counting and by counting you should know that, for instance, 4 is different from 7 and 2+2, which is equal to 4, is different from 7… but it depends!

In everyday life, there are various situations in which it happens to “count” in a different way from what is usually done; however, nobody is less serene. Perhaps somebody would be less serene if he knew it is all about Math, in particular about Modular Arithmetic… but this is a well-kept secret.
Three kids (Annie, Joe and Charlie) are counting out to decide who is going to play first: they are reciting the rhyme “A-u-lì-u-lè-ka-tà-mu-sé-…”. In order, they are pointing one of them for each syllable they are saying until the rhyme ends and the last syllable… chooses the first to play. Assume none of them is cheating, which it may be if syllables overlap or if they swallow their words. We just need to know how many syllables there are in the rhyme so that we could guess which of the three kids is going to play first. This is a rhyme made up of 27 syllables. If Annie starts to recite it and they go on in alphabetical order, the last syllable chooses Charlie.
This is a very strange arithmetic. In fact, a rhyme with 27 syllables has the same effect as that with 3 syllables (or with 6, 9 or 99): it is an arithmetic for which 27 is equal to 3, 6, 9…
If the rhyme had 28 syllables, we would find out that 28 is equal to 25 and 22…, to 13 and 7 and 4 and even to 1. Thus, 2+2 is equal to 4, but also to 1 (or, if you prefer, to 25 or 28).
It is as if all multiples of 3 were equal to zero and we kept track of the remainder when we divide a number by 3. There are the numbers which are multiples of 3 (which correspond to Charlie), those with remainder one when divided by 3 (Annie) and those with remainder 2 when divided by 3 (Joe).
We do not need to go back to our childhood to discover such an arithmetic. Just think of the arithmetic of a clock, where the role of the number 3 in the previous example is taken by the number 12: we thus refer to an arithmetic modulo 12. We can also talk about the arithmetic of the the days of the week (modulo 7) or, more simply, that of the odd and the even numbers (modulo 2). They are different ways of counting in situations when something repeats periodically.
In general, very simple concepts are very deep too. We should not be too much surprised if, since childhood, we are familiar with modular arithmetic (even if we are not aware of it) which, at the same time, is the foundation of current theoretical research in Number Theory. It is also the foundation of some of the most recent applications, which progress in Cryptography has introduced in everyday life, from ATM cards to the e-commerce.